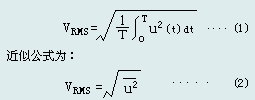百科:真有效值即为“真正有效值”之意,英文缩写为“TRMS”,有的文献也称为真均方根值,我们先回忆一下交流电压的有效值的表达式,它的定义如下:
我们对式(1)进行变换,两边平方,并令
就得到真有效值电压的另一种表达式
从(3)式即得,对输入电压依次进行“取绝对值→平方/除法→取平均值”运算,也能得到交流电压的有效值,而且这公式更有使用价值。举例说明:假如要测量一电压变化范围是0.1V-10V,平方后u=10mV—100V,这就要求平方器具有相当大的动态范围(10000:1),这样的平方电路误差就可能超过1mV,要平方器能输出100V的电压,技术上是难以实现的。如果使用式(3)的既便于设计电路,也能保证了准确度。因此,目前大多数的集成单片真有效值/直流转换器均采用式(3)的原理而设计。 真有效值仪表的的核心器件是TRMS/DC转换器。现在市场上这类单片的集成芯片很多,真有效值仪表普遍使用了这类集成电路。单片集成电路具有集成度高、功能完善,外围元件少,电路连接简单、电性能指标容易保证等诸多优点,这类芯片能准确、实时测量各种电压波形的有效值,无须考虑波形参数和失真,这些性能是平均值仪表无法比拟的。
福禄克官方内部数据:为什么要使用真有效值?
“RMS”“root-mean-square”(均方根)。它来源于用于计算任意 AC 波形的有效值(或发热值)的一个数学公式。在电气术语中,ac rms 值等同于特定波形(电压或电流)的 dc 发热值。例如,如果电炉中的电阻发热元件在 240 V ac rms 下的额定发热量为 15 kW,则如果施加 240 V dc 电压而不是 ac 电压,就会得到相同的热量。
熔断器、母排、导线和断路器的热元件等部件都以有效值 (rms) 电流来标明额定值,因为它们的主限制作用与热量耗散有关。如果我们想检查一个电路有无过载,则需要测量 rms 电流,并将测量值与有关部件的额定值进行比较。
如果一个钳形表被标明可响应真有效值,这意味着该工具的内部电路会根据 rms 公式来计算发热值。这种方法可给出正确的发热值,而不管电流波形如何。
某些廉价的钳形表,没有真有效值电路,而使用简化法来得到均方根值。这些仪表被归为“平均响应-真有效值指示”型。这些仪表可捕获 ac 波形经过整流的平均值,并将数值乘以 1.1 以计算出 rms 值。换言之,它们所显示的值不是一个真实值,而是一个基于波形的假设计算出来的值。平均响应方法适用于纯粹正弦波,但在波形因可调速驱动器或计算机而发生波形失真时,可能会导致高达 40 % 的较大读数误差。下表给出了两种不同类型仪表响应不同波形的方式的一些示例。
钳形表有两种外形。最常见的类型是一体式钳形表,它包括钳口,读数显示,和嵌于独立单元内的测量电路。这类型的钳形表包括,Fluke 335,336和337,381。可在前面板上看到真有效值字样。
第二种类型是由变流器(CT)型附件组成,它与数字万用表共同使用。这类型的钳形表包括 Fluke i200s、80i-400 和 80i-600A。钳形表的钳口将所测导线围住,这充当了变压器的单圈初级线圈。次级线圈有 1000 匝,这就把所测电流除以了 1000;如果所测电流为安培级,那么就转化为毫安级。当钳形表的输出线插到万用表的交流毫安接口,这样,万用表的十位读数就是所测的安培值。